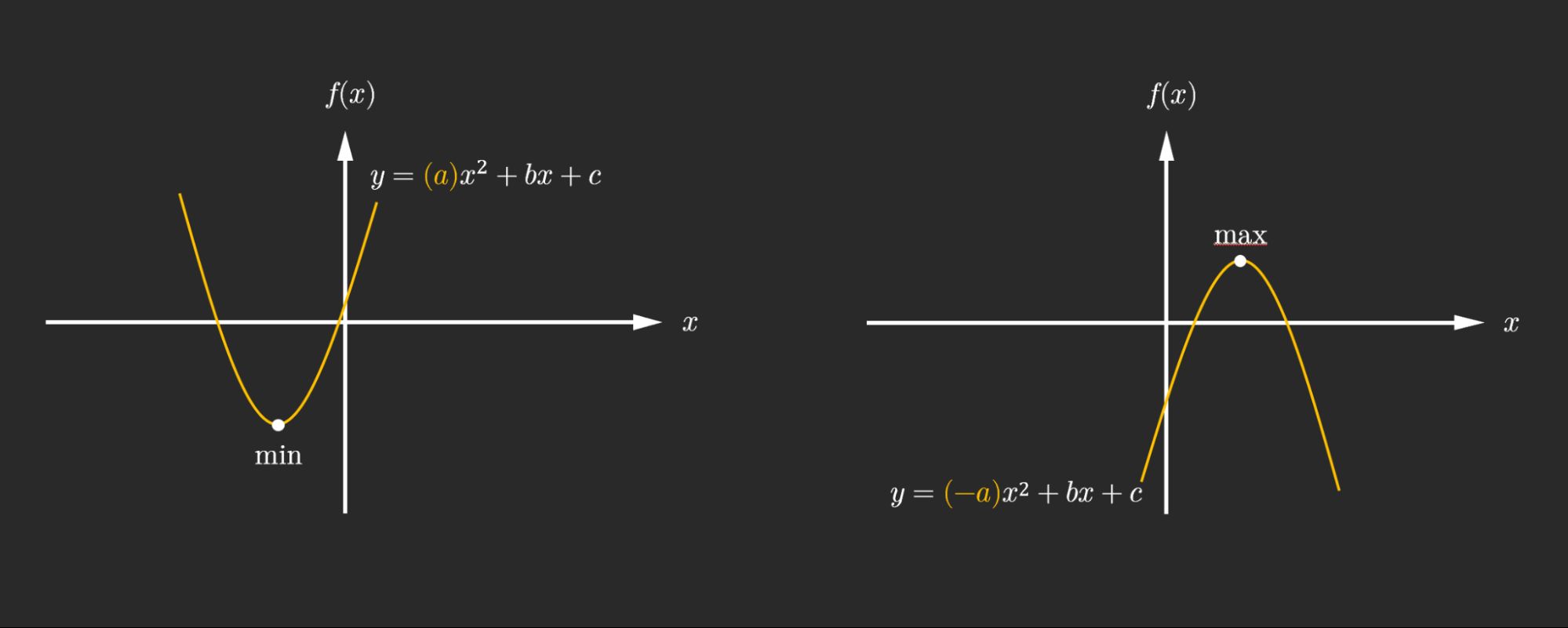Your next
Start now with courses in Mathematics AA and Computer Science.
Questionbank
Worksheets
Dictionary
Save for later
Coursework
Lessons
Questionbank
Worksheets
Dictionary
Lessons
Looking for a combined solution?
Mathematics AA
Computer Science
Want to take your Maths and Comp-Sci to the next level? Look no further
Plus, have you seen our worked markschemes & questions?
Try it!
Content worth
0
+
Extended Essays
Developed by
0
Students
With roughly
0
Hours of work
Our Lessons have it in them
Lesson Content
Heading 1
Heading 2
Heading 3
Heading 4
Heading 5
Heading 6
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur.
Block quote
Ordered list
- Item 1
- Item 2
- Item 3
Unordered list
- Item A
- Item B
- Item C
Bold text
Emphasis
Superscript
Subscript
Heading 1
Heading 2
Heading 3
Heading 4
Heading 5
Heading 6
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur.
Block quote
Ordered list
- Item 1
- Item 2
- Item 3
Unordered list
- Item A
- Item B
- Item C
Bold text
Emphasis
Superscript
Subscript
2.3-6 | Forms of Quadratics
Standard form
As we have explored linear functions (polynomials to the first power), we will now look into quadratic functions (polynomials to the second power).
Quadratics are composed of 3 terms: \(x^2\), \(x\), and constant terms. In the standard form of quadratics, they are represented as follows:
\[f(x) = ax^2 + bx + c\]
where \(c\) is the y-intercept, and \(a\) indicates whether the quadratic points upwards or downwards. Specifically, if \(a\) is negative, then the parabola opens up downwards, but it opens upwards when \(a\) is positive. I.e. the function has a maximum (range) when \(a\) is negative, and the function has a minimum (range) when \(a\) is positive:
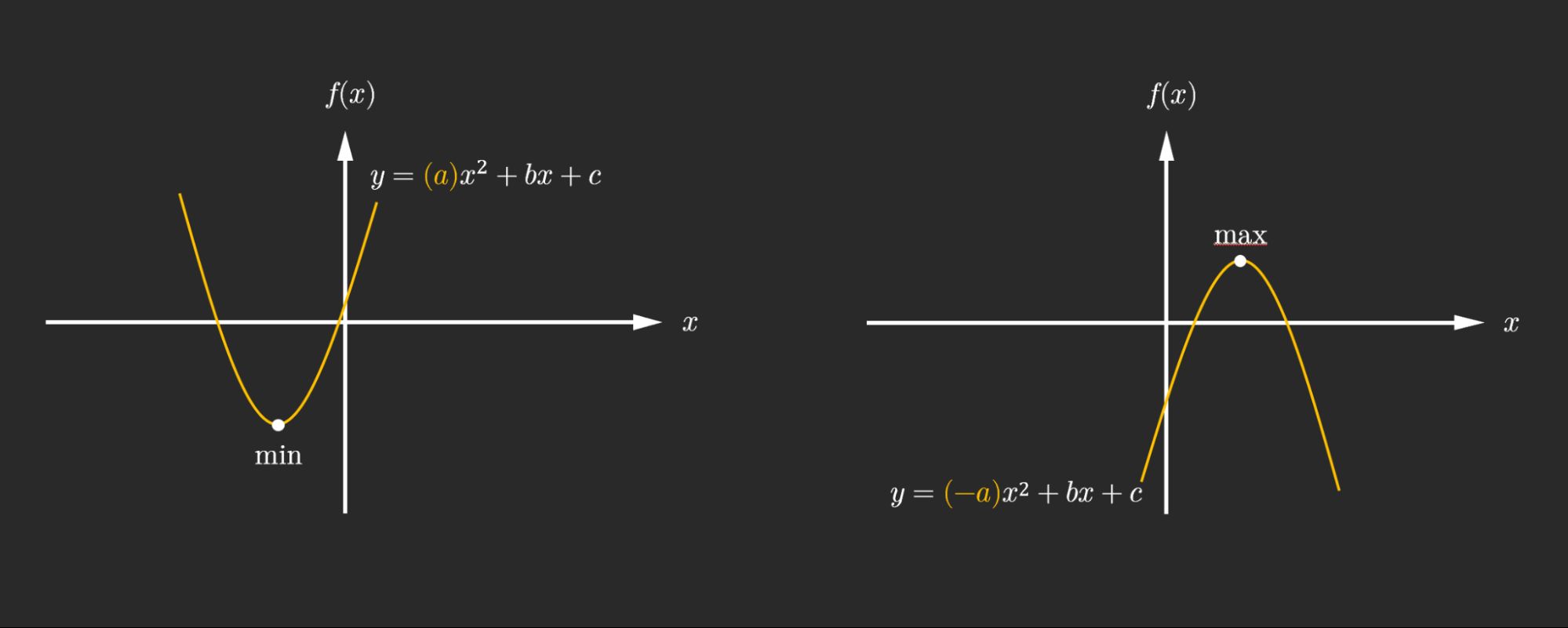
Another useful hint we can derive from the standard form of quadratics is the line of symmetry. It can be noticed that the parabolic shapes that quadratics generate are symmetrical, with a line of symmetry traveling through the center vertically. To determine the equation of the line of symmetry (which can also be useful in finding the vertex i.e. the minimum and maximum points of the function– since the vertices lie on the line of symmetry), we can make use of the coefficients as follows:
\[x = -{b \over 2a}\]
This provides the line of symmetry. To find the vertex, we can use this value for \(x\), and plug it in for \(f(x)\), such that the y-value of the function at \(x\) can be determined:
\[\text{Coordinates of Vertex} = (-{b \over 2a}, f(-{b \over 2a}))\]
Factored form
This form is key in identifying the roots of the quadratic. The factored form is represented as follows:
\[f(x) = a(x-p)(x-q)\]
This is special, because when the y-value aka \(f(x) = 0\), the \(x\) value provides the intersection with the x-axis, i.e. the roots.
Therefore, if the value of the function is 0, it means that \(x\) is a root. In factored form, if \(x=p\) or \(x=q\), it would cause either \(q-q=0\) or \(p-p=0\), i.e. the value of the function being 0, rendering \(x=p\) or \(x=q\) roots of the function \(f(x)\).
To get to this form, it is crucial to understand how to factor quadratics– going from standard form to factored form. Although there is indeed a formula (the quadratic formula), you cannot always just plug in numbers there, as paper 1 does not allow a calculator to be used, causing calculations to become extremely tedious. Therefore, factoring is highly important.
Going from standard form to factored form has a basic procedure which can be applied to any given quadratic \(ax^2 + bx + c\). However, it must be kept in mind that although all quadratics can be factored, not all of them can be factored with nice, integer numbers. Therefore if you cannot easily factor the quadratic, you have most likely either made a mistake, or it is a paper 2 or 3 question where you may use your calculator to calculate/graph roots.
-
Multiply \(a\) and \(c\) to get \(ac\)
-
Find 2 numbers that multiply to \(ac\) and add up to \(b\) simultaneously
-
Letting these 2 numbers in step \(2\) be \(p\) and \(q\), separate \(bx\) to \(px + qx\)
-
Factor like terms
-
Factor like terms again
This may seem confusing, but it really is quite simple. It can easily be visualized through an example:
Solve \(x^2 - 5x + 6 = 0\)
In this case, \(a = 1\), \(b = -5\), \(c = 6\). Therefore:
\begin{align}
ac &= 1 \times 6\\
ac &= 6\\
\end{align}
Now we must find 2 numbers that multiply to \(6\), but add up to \(-5\).
This is possible with the numbers \(-2\) and \(-3\), because \((-2) \times (-3) = 6\), and \((-2) + (-3) = - 2 - 3 = - 5\).
Hence, we separate \(-5x\) into \(-2x-3x\):
\begin{align}
x^2 - 5x + 6 &= 0\\
x^2 - 2x - 3x + 6 &= 0\\
\end{align}
We can notice that the leftmost 2 terms have an \(x\) in common, and the right-most 2 terms have a 3 in common (instead of 3 we can factor negative 3, such that the minus corresponds in the same way as the leftmost terms):
\begin{align}
x^2 - 2x - 3x + 6 &= 0\\
x(x - 2) - 3(x - 2) &= 0\\
\end{align}
Now we can factor a second time, as we can notice that the term \((x-2)\) is common for both terms:
\begin{align}
x(x - 2) - 3(x - 2) &= 0\\
(x - 2)(x - 3) &= 0\\
\end{align}
Hence, we have achieved factored form.
We can also easily tell that the equation would be satisfied by \(x = 2\) and \(x = 3\), because then the equation would lead to \(0 = 0\) which is a true statement.
Therefore, \(x = 2\) and \(x = 3\) are roots of the function \(f(x) = x^2 - 5x + 6 = 0\).
Vertex Form
This is the 3rd form of quadratics which should be studied. Vertex form is represented as follows:
\[f(x) = a(x - h) + k\]
Through this form, the coordinates of the vertex (i.e. the minimum or maximum point of the quadratic) can be identified as \((h,k)\).
In the exam, you can be explicitly asked to use vertex form to determine the vertex.
Going from standard form to vertex form is also systematic, such that it just requires a number of basic steps given a quadratic \(ax^2 + bx + c\):
-
Take out the Greatest Common Factor (GCF) of the first two terms \(a\) and \(b\), such that \(x^2\) no longer has a coefficient, and the equation resembles the form:
\[p(x^2 + qx) + c)\] -
Take the number \(({q \over 2})^2\) (half of q, squared). Add and subtract this number simultaneously, such that the equation resembles the form:
\[p(x^2 + qx + ({q \over 2})^2 - ({q \over 2})^2) + c)\] -
Multiply \(({q \over 2})^2\) by \(p\) to take it out of the brackets, such that the equation resembles the form:
\[p(x^2 + qx + ({q \over 2})^2) + c - ({q \over 2})^2 \times p)\] -
After writing down \(p\) open-bracket, write down \(x\), the sign after \(x^2\), and \({q \over 2}\) close-bracket, all squared, and then the rest of the remaining terms, such that the equation resembles the form:
\[p(x + ({q \over 2}))^2 + c - ({q \over 2})^2 \times p\] -
Hence, vertex form has been achieved, with the vertex being \((-{q \over 2}, (c - ({q \over 2})^2 \times p)\), where \(h = -{q \over 2}\) and \(k = c - (({q \over 2})^2 \times p)\)
This probably seems super confusing just because of the number of variables, but this is simply the generalized form. The best way to understand this would be through an example:
Given the function \(f(x) = 2x^2 + 8x - 5\), find the coordinates of the vertex through vertex form.
Taking the GCF of the coefficients of \(2x^2\) and \(8x\) is \(2\). Hence:
\begin{align}
& 2x^2 + 8x - 5\\
&= 2(x^2 + 4x) - 5\\
\end{align}
Taking half of \(4\) and squaring, leads to \(({4 \over 2})^2 = 2^2\). Adding and subtracting:
\begin{align}
&= 2(x^2 + 4x + 2^2 - 2^2) - 5\\
\end{align}
Taking the \(-2^2\) out of the brackets, we must multiply it by the coefficient on the bracket, which is \(2\):
\begin{align}
&= 2(x^2 + 4x + 2^2 - 2^2) - 5\\
&= 2(x^2 + 4x + 2^2) - 5 - (2 \times 2^2)\\
\end{align}
Writing down according to step 4 and simplifying:
\begin{align}
&= 2(x^2 + 4x + 2^2) - 5 - (2 \times 2^2)\\
&= 2(x + 2)^2 - 5 - (2 \times 2^2)\\
&= 2(x + 2)^2 - 5 - (2 \times 4)\\
&= 2(x + 2)^2 - 5 - 8\\
&= 2(x + 2)^2 - 13\\
\end{align}
Hence, vertex form has been achieved, with the coordinates of the vertex being \((-2,-13)\).
Linked Questions
SL-SAM-AA01
SL-SAM-AA03
Made by students from
